Claude Shannon

Introduction
- Claude Elwood Shannon is considered as the founding father of electronic
communications age. He is an American mathematical engineer, whose work
on technical and engineering problems within the communications industry,
laying the groundwork for both the computer industry and telecommunications.
After Shannon noticed the similarity between Boolean algebra and the telephone
switching circuits, he applied Boolean algebra to electrical systems at the
Massachusetts Institute of technology (MIT) in 1940. Later he joined the staff
of Bell Telephone Laboratories in 1942. While working at Bell Laboratories, he
formulated a theory explaining the communication of information and worked on
the problem of most efficiently transmitting information. The mathematical
theory of communication was the climax of Shannon's mathematical and engineering
investigations. The concept of entropy was an important feature of Shannon's
theory, which he demonstrated to be equivalent to a shortage in the information
content (a degree of uncertainty) in a message.
Background & Family
- Claude Elwood Shannon was born in Gaylord, Michigan, on April 30, 1916,
to Claude Elwood and Mabel Wolf Shannon. Shannon's father, Claude, was a judge
at Gaylord which was a little town of about three thousands in Michigan.
Although he didn't work in the field of mathematics, he was clever mathematically
and knew what he was talking about. As for his mother, Mabel, who was the
principal of the high school in Gaylord. Even though there wasn't much
scientific influence from Shannon's father, most of it came from his grandfather.
Shannon's grandfather was an inventor and a farmer. He invented the washing
machine along with many others farming machinery. On March 27, 1949, Shannon
married Mary Elizabeth Moore and together they have three children; Robert
James, Andrew Moore, and Margarita Catherine.
Invention
- Just a few miles from the Massachusetts Institute of Technology was Shannon's
large house. The house is filled with musical instruments such as five pianos
and 30 other instruments, from piccolos to trumpets. The chess-playing machines
include one that moves the pieces with a three-fingered arm, beep and makes
wry comments. A chair lift that he built to take his three children 600 feet
down to the lakeside has been taken down now that they are grown. Shannon's
lifelong fascination with balance and controlled instability has led him to
design a unicycle with an off-center wheel to keep the rider steady while
juggling. Shannon love to juggle since he was a kid. In his toy room is a
machine with soft beanbag hands that juggle steel balls. His juggling
masterpiece is a tiny stage on which three clowns juggle 11 rings, 7 balls,
and 5 clubs, all driven by an invisible mechanism of clockwork and rods.
Education
- Shannon was educated at Michigan University in 1936, where he earned his B.S.
degree. Later he went to Massachusetts Institute of Technology, where he
studied both electrical engineering and mathematics, receiving a master's
degree and a doctorate. For his master's degree in electrical engineering, he
applied George Boole's logical algebra to the problem of electrical switching.
During that time Boole's system for logically manipulating 0 and 1 was little
known, but it is now the nervous system of every computer in the world. Then
for his doctorate, he applied mathematics to genetics. Shannon received both
his master's degree and his doctorate in 1940.
Awards & Honors
- He was named a National Research Fellow and spent a year at Princeton's
Institute for Advanced Study.
In addition to his work at Bell Laboratories, Shannon has spent many years
teaching at MIT. He was a visiting professor of electrical communication in
1956, and then in 1957 he was named professor of communications sciences and
mathematics. In 1958 he returned to MIT as Donner Professor of Science until
he retired. Throughout Shannon's life, he has received many honors including
the Morris Liebmann Memorial award in 1949, the Ballantine Medal in 1955, and
the Merin J. Kelly Award of the American Institute of Electrical Engineers in
1962. In addition, he was awarded the National Medal of science in 1966, as
well as the Medal of Honor that same year from the Institute of Electrical and
Electronics Engineers. Likewise, he received the Jaquard award in 1978, the
John Fritz Medal in 1983, and the Kyoto Prize in Basic Science in 1985, along
with numerous other prizes and over a dozen honorary degrees. Also, he is a
member of the American Academy of Arts and Sciences, the National Academy of
Sciences, the National Academy of Engineering, the American Philosophical
Society, and the Royal Society of London.
Classic Paper
- Besides Shannon's theory of communication, he published a classic paper
"A Symbolic Analysis of Relay and Switching Circuits." This paper point out
the identity between the two "truth values" of symbolic logic and the binary
values 1 and 0 of electronic circuits. Shannon showed how a "logic machine"
could be built using switching circuits corresponding to the propositions of
Boolean algebra.
Work
- Shannon joined Bell Telephone Laboratories as a research
mathematician in 1941. He worked on the problem of most efficiently
transmitting information. Soon he discovered the similarity between boolean
algebra and telephone switching circuits. By 1948, Shannon turned his efforts
toward a fundamental understanding of the problem and had evolved a method of
expressing information in quantitative form. The fundamental unit of
information is a yes-no situation. Either something is or is not. This can
be easily expressed in Boolean two-value binary algebra by 1 and 0, so that
1 means "on" when the switch is closed and the power is on, and 0 means "off"
when the switch is open and power is off. Under these circumstances, 1 and 0
are binary digits, a phrase that can be shortened to "bits." Thus the unit of
information is the bit. A more complicated information can be viewed as built
up out of combinations of bits. For example, the game of "twenty questions,"
shows how quite complicated objects can be identified in twenty bits or less,
using the rules of the game. Also, something much more elaborate, such as is
seen by the human eye, can also be measured in bits. Since each cell of the
retina might be viewed as recording "light" or "dark" ("yes" or "no") and it
is the combination of these yes-no situations that makes up the complete
picture.
Entropy
- One of the most important feature of Shannon's theory was the concept of
entropy, which he demonstrated to be equivalent to a shortage in the
information content in a message. According to the second law of
thermodynamics, as in the 19th century, entropy is the degree of randomness
in any system always increased. Thus many sentences could be significantly
shortened without losing their meaning. Shannon proved that in a noisy
conversation, signal could always be send without distortion. If the message
is encoded in such a way that it is self-checking, signals will be received with
the same accuracy as if there were no interference on the line. A language,
for example, has a built in error-correcting code. Therefore, a noisy party
conversation is only partly clear because half the language is redundant.
Shannon's method were soon seen to have applications not only to computer
design but to virtually very subject in which language was important such as
linguistic, psychology, cryptography and phonetics.
Achievement :
I. http://www2.eis.net.au/~karlerik/Information.html#Shannon : Information Theory:
One of the basic postulates of information theory is that information can be treated like a measurable physical quantity, such as density or mass. The theory has widely applied by communication engineers and some of its concepts have found application in psychology and linguistics.
The basic elements of any general communications system include
- a source of information which is a transmitting device that transforms the information or "message" into a form suitable for transmission by a particular means.
- the means or channel over which the message is transmitted.
- a receiving device which decodes the message back into some approximation of its original form.
- the destination or intended recipient of the message.
- a source of noise (i.e., interference or distortion) which changes the message in unpredictable ways during transmission.
It is important to note that "information" as understood in information theory has nothing to do with any inherent meaning in a message.
It is rather a degree of order, or nonrandomness, that can be measured and treated mathematically much as mass or energy or other physical quantities are.
A mathematical characterization of the generalized communication system yields a number of important quantities, including
- the rate at which information is produced at the source.
- the capacity of the channel for handling information.
- the average amount of information in a message of any particular type.
To a large extent the techniques used with information theory are drawn from the mathematical science of probability. Estimates of the accuracy of a given transmission of information under known conditions of noise interference, for example, are probabilistic, as are the numerous approaches to encoding and decoding that have been developed to reduce uncertainty or error to minimal levels.
Information and Uncertainty are technical terms that describe any process that selects one or more objects from a set of objects. We won't be dealing with the meaning or implications of the information since nobody knows how to do that mathematically.
Suppose we have a device that can produce 3 symbols, A, B, or C. As we wait for the next symbol, we are uncertain as to which symbol it will produce. Once a symbol appears and we see it, our uncertainty decreases, and we remark that we have received some information. That is, information is a decrease in uncertainty.
How should uncertainty be measured? The simplest way should be to say that we have an "uncertainty of 3 symbols". This would work well until we begin to watch a second device at the same time, which, let us imagine, produces symbols 1 and 2. The second device gives us an "uncertainty of 2 symbols". If we combine the devices into one device, there are six possibilities, A1, A2, B1, B2, C1, C2. This device has an "uncertainty of 6 symbols". This is not the way we usually think about information, for if we receive two books, we would prefer to say that we received twice as much information than from one book. That is, we would like our measure to be additive.
Shannon is as the founding father of electronic communications age since he noticed and discovered the similarity between Boolean algebra and the telephone switching circuits. For example, the fundamental unit of information is a yes-no situation. Either something is or is not. This can be easily expressed in Boolean two-value binary algebra by 1 and 0, so that 1 means "on" when the switch is closed and the power is on, and 0 means "off" when the switch is open and power is off.
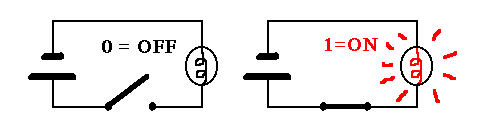
Under these circumstances, 1 and 0 are binary digits, a phrase that can be shortened to "bits." Thus the unit of information is the bit. A more complicated information can be viewed as built up out of combinations of bits.
By 1948, He turned his efforts toward a fundamental understanding of the problem and had evolved a method of expressing information in quantitative form.
Conclusion
- Shannon is a living legend at seventy-nine. What made him stand out from
others mathematician is that he never content just to know a topic well. He
constantly rearranges it, tries it in different settings, until he gets it
into form in which he explain it, sometime literally, to the people in the
street. He is the founding father who laid down its most important
principles. His contributions are saluted by the world and his
work not only helped translate circuit design from an art into a science,
but its central tenet.
This page is a cached copy on a different server than the original (http://www.nyu.edu/pages/linguistics/courses/v610003/shan.html) site. The original site should be used at all times except when unavailable. No copyright was included in the original document when this was duplicated, but I will respect the original author, if they requst for me to remove this copy. Maintainer of locally cached copy can be reached here.